請先下載練習檔

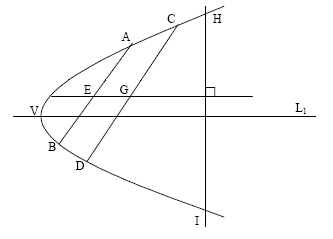
A.作拋物線的頂點

1. 任意作兩平行弦AB//CD 。
2. 分別取AB,CD 之中點，令其為E、G。
3. 作直線EG，此直線為拋物線的直徑，故直線EG 平行於對稱軸。
4. 拋物線上取一點H，作HI ⊥ EG ，交拋物線於另一點I。作HI 之中垂線L1，L₁ 即為對稱軸。
5. L1 與拋物線的交點即為頂點，設其為V。

• 【原理】拋物線上一組平行弦中點的集合為一射線，此射線稱為拋物線的一個直徑，直徑平行對稱軸。

完成圖檔

B.作拋物線的焦點

1. 在拋物線外作直線L₂⊥ L₁，設垂足為J。
2. 在直線L₂ 上取兩點K 、M ， 使得JK = KM = JV 。
3. 作直線MV，交拋物線於另一點N。
4. 作NO ⊥L₁，且交L₁ 於點F，F 即為拋物線的焦點。

• 【原理】拋物線焦點到頂點的距離為正焦弦長的四分之一 。

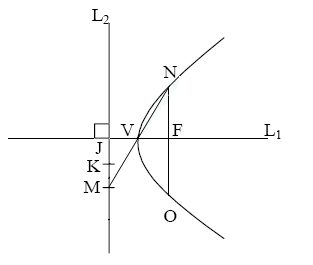
【證明】依作圖ΔVJM ~ΔVFN ，則VJ:JM=VF:FN=1: 2 ，

因為拋物線焦點至頂點的距離為正焦弦長的四分之一

所以點F 為焦點。(JV≠VF)

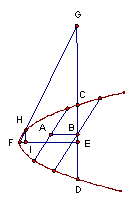
拋物線另解：

(1) 畫拋物線的兩條平行弦，並分別作它們的中點A,B，連線AB。
(2) 過B作AB的垂線交拋物線於C、D兩點。
(3) 作CD的中點E，並過E作CD的垂線交拋物線於一點F，此點為拋物線的頂點。直線EF即為物線的對稱軸。
(4) 在直線CD上取一點G，使得EG＝2EF。並連直線FG交拋物線的另一交點H。
(5) 過H作EF的垂線，並交直線EF於I。則I即為拋物線的焦點。

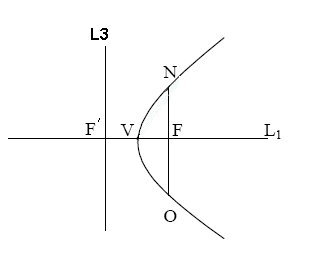
C.作拋物線的準線

D.過拋物線上任一點作切線

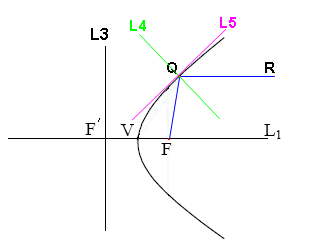
1. 設拋物線上一點Q，作FQ。
2. 作直線QR//L₁。
3. 作∠FQR 的平分線L4。
4. 過點Q 作直線L₅⊥ L₄，直線L₅ 即為過點Q的切線。

• 【說明】直接運用拋物線的光學性質。

E.過拋物線外一點作切線

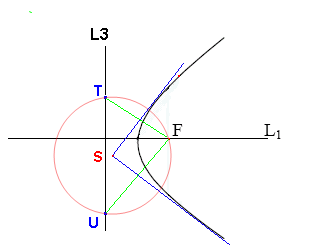
1. 設拋物線外一點S，在準線上取兩點T、U，使得ST = SU = SF 。
2. 分別作TF,UF 的中垂線L₆、L₇，直線L₆、L₇即為過點S 的兩切線。

• 【原理】利用拋物線的定義，即拋物線上的點到焦點的距離等於到準線的距離，以確定切點在拋物線上，同時利用一線段其中垂線上的點，到此線段兩端點的距離相等之性質，確定切線的位置。